Typeclasses II, Batteries Included

Introduction

This page aims to highlight some of main typeclasses available in Prelude. The diagram below, from the 2010 Haskell report is a useful summary. Arrows from A to B indicate that B has a typeclass constraint of A.

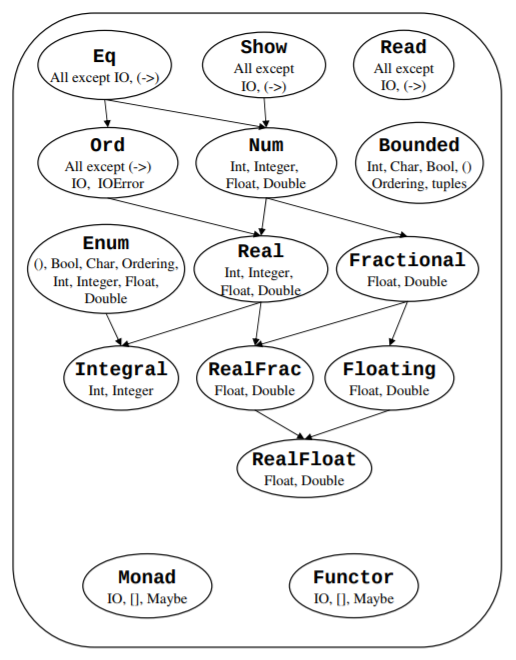
Batteries included: Some common typeclasses

These typeclasses are all part of the Haskell 2010 standard. Note that the type hierarchy given there no longer exactly that in the GHC Prelude.

Eq

The Eq class defines equality (==) and inequality (/=). All basic datatypes in Prelude are instances of Eq.

class  Eq a  where  
  (==), (/=)  ::  a -> a -> Bool  

  x /= y  = not (x == y)  
  x == y  = not (x /= y)

Note that it suffices to define either (==) or (/=), but not both. The compiler can use the presence of one to compute the value of the other. For more on the properties of Eq, see here.

Ord

The Ord typeclass defines functions that compare values. Ordering can be represented in Haskell using the built-in type

data Ordering = LT | EQ | GT

The typeclass definition is below. Note the constraint Eq a - this allows us to use equality testing in the definition below.

class  (Eq a) => Ord a  where
  compare              :: a -> a -> Ordering  
  (<), (<=), (>=), (>) :: a -> a -> Bool  
  max, min             :: a -> a -> a 

  compare x y | x == y    = EQ  
              | x <= y    = LT  
              | otherwise = GT  

  x <= y  = compare x y /= GT  
  x <  y  = compare x y == LT  
  x >= y  = compare x y /= LT  
  x >  y  = compare x y == GT  

  max x y | x <= y    =  y  
          | otherwise =  x  
  min x y | x <= y    =  x  
          | otherwise =  y

Defining either compare or <= is sufficient for a minimal complete definition. See here for more properties.

Show

The typeclass Show handles conversion of values to readable Strings. This is the machinery used whenever we write deriving (Show) for custom types.

class  Show a  where  
    showsPrec :: Int -> a -> ShowS  
    show      :: a -> String  
    showList  :: [a] -> ShowS  
 
    showsPrec _ x s   = show x ++ s  
    show x            = showsPrec 0 x ""  
    -- ... default decl for showList given in Prelude

Defining either showsPrec or show is sufficient for a minimal completion definition. See here for more properties.

Enum

The typeclass Enum defines operations on sequentially ordered types. This is the typeclass used in Haskell’s translation of values like [n..m].

The default Prelude declaration is below.

class  Enum a  where  
    succ, pred     :: a -> a   -- Successor / predecessor of a value
    toEnum         :: Int -> a            -- Convert from an Int
    fromEnum       :: a -> Int            -- Convert to an Int 
    enumFrom       :: a -> [a]            -- [n..]  
    enumFromThen   :: a -> a -> [a]       -- [n,n'..]  
    enumFromTo     :: a -> a -> [a]       -- [n..m]  
    enumFromThenTo :: a -> a -> a -> [a]  -- [n,n'..m]  

    succ                   = toEnum . (+ 1)  . fromEnum
    pred                   = toEnum . (subtract 1) . fromEnum
    enumFrom x             = map toEnum [fromEnum x ..]
    enumFromThen x y       = map toEnum [fromEnum x, fromEnum y ..]
    enumFromTo x y         = map toEnum [fromEnum x .. fromEnum y]
    enumFromThenTo x1 x2 y = map toEnum [fromEnum x1, fromEnum x2 .. fromEnum y]

It suffices to define toEnum and fromEnum for a complete definition. See here for more properties and documentation.

Num

The typeclass Num defines the basic numeric class. The default Prelude declaration is below.

class  Num a  where
    (+), (-), (*)       :: a -> a -> a
    -- | Unary negation.
    negate              :: a -> a
    -- | Absolute value.
    abs                 :: a -> a
    -- | Sign of a number.
    signum              :: a -> a
    -- | Conversion from an 'Integer'.
    fromInteger         :: Integer -> a

    x - y               = x + negate y
    negate x            = 0 - x

For a minimal complete definition, we must define (+), (*), abs, signum, fromInteger, and negate (or (-)).

References

• https://www.haskell.org/onlinereport/haskell2010/haskellch6.html
• http://hackage.haskell.org/package/base-4.12.0.0/docs/Prelude.html#t:Read